How To Find Solution Sets

Solution Sets of linear systems

What is a solution gear up in algebra

A solution ready in algebra refers to the set of values which inputted into a organization of equations correctly solve such system. In other words, these values satisfy the equality of the equations contained in the system nosotros are trying to solve and so, the list of the respective value for each unknown variable in a system conforms the complete fix of solutions.

At this betoken, we are no strangers to the idea of solving a prepare of linear equations, we have done it in dissimilar ways through by lessons in our Linear Algebra class, such as in the lesson on solving systems of linear equations past graphing or the lesson about solving a linear arrangement with matrices using Gaussian elimination.

Nosotros volition continue to use such techniques (mostly Gaussian elimination, also known equally row reduction) throughout our lesson of today to find a linear system solution, only before nosotros go on on to that information technology is imperative nosotros finally get to know the types of linear systems of equations that we tin find in our bug:

A system of linear equations is homogeneous if nosotros tin write its matrix equation in the form $Ax=0$ . On the other paw, a system of linear equations is nonhomogeneous if we tin write its matrix equation in the class $Ax=b$ .

We can express solution sets of linear systems in parametric vector form, merely the type of organization nosotros have to piece of work with will make a departure in the blazon of solutions we tin obtain:

• Types of solutions a homogeneous arrangement tin accept in parametric vector form:
• With one free variable: $10=television$
• With two free variables: $10=su+tv$
• With due north free variables: $x=av_{1}+bv_{2}+...+nvn$


• Types of solutions a nonhomogeneous organization can take in a parametric vector class:
• With 1 free variable: $x=p+tv set$
• With two complimentary variables: $x=p+su+boob tube$
• With north free variables: $ten=p+av_{i}+bv_{2}+...+nv_{due north}$

Where x represents the column vector containing all of the corresponding unknown variables from the linear arrangement. $u$ , $v$ and $v_{ane, 2 ... n}$ correspond the cavalcade vectors formed past the coefficients of each unknown variable in each equation from the system; while $s$ , $t$ and $a$ , $b$ , ... , $n$ are the gratuitous variables.

For the case of nonhomogeneous systems you lot will accept an extra vector coming out in the solutions, this extra vector is what we have named $p$ above.

How to find a solution set of an equation

The basic steps to follow when computing solution sets for a system of linear equations are:

1. Catechumen the linear system into a matrix equation
2. Rewrite the matrix equation as an augmented matrix
3. Compute the reduced echelon form of the augmented matrix using Gaussian elimination
4. The reduced echelon form of the matrix will provide the values (or expressions) for the unknown variables, use these solutions to write down the parametric vector equation form which volition incorporate the complete ready of solutions for the arrangement.

All of these steps will be explained in item in the exercise examples provided in the last section of this lesson. For now, information technology is important that if you lot accept any doubt on how to piece of work through any of the steps mentioned above, you revisit the next by lessons: representing a linear system as a matrix, row reduction and echelon forms and matrix equation $Ax=b$ .

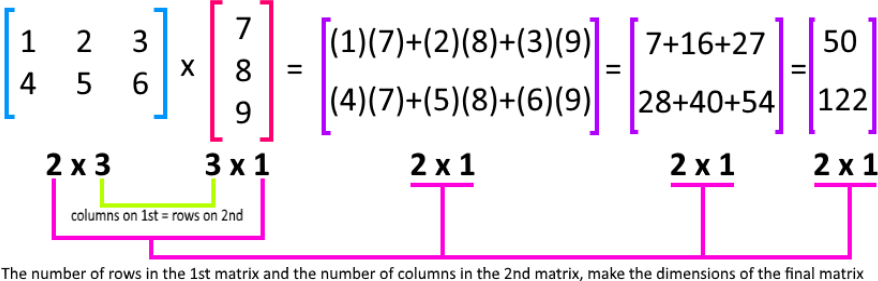
Before we continue onto the next section of this lesson, permit us take a quick review of something we have been mentioning many times throughout our lessons: matrix multiplication!
Beneath you tin discover the diagram containing the full general rules for matrix multiplication. You must be already familiarized with this diagram since we take included it in lessons before. The reason why nosotros bring this one upwards, is that in order to produce matrix equations we will be looking into matrix multiplications (the matrix equations $Ax=0$ and $Ax=b$ are matrix multiplications themselves!), and so, just accept the adjacent diagram every bit a reference for later parts of this lesson where you volition be working on exercise examples.

Equation ane: Matrix multiplication

What is a picayune solution in linear algebra

A vector is called trivial if all its coordinates are 0, for instance, if it is the aught vector
In Linear Algebra we are non interested in only finding one solution to a system of linear equations. Nosotros are interested in all possible solutions. In particular, homogeneous systems of equations (see in a higher place) are very of import. The important question for a homogeneous organisation is whether or not at that place is any non-petty solution, i. e. whether there is any solution other than the trivial i. Sometimes there will exist, sometimes at that place wont. Paradoxically, its actually the case where the trivial solution is the but possible one that is the nigh of import. This state of affairs is described by ane of the near important words in the whole course.

Find solution set

For this final section of our lesson of today, we will be looking for the solutions sets of linear systems. Every bit usual, we will be using annotation of matrices in society to notice the corresponding matrix solution set required in each case.

Case 1

Detect the solution prepare of the homogeneous system in parametric vector form:

Equation 2: System of linear equations

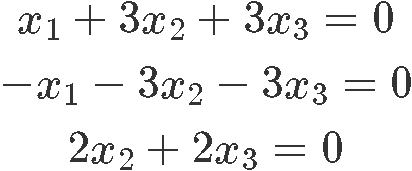
As nosotros accept been doing so for a few lessons now, we transform this system into an augmented matrix and then row reduce it until nosotros obtain its reduced echelon grade in gild to discover the last expressions for the variables of the system:

Equation three: Row reducing the augmented matrix

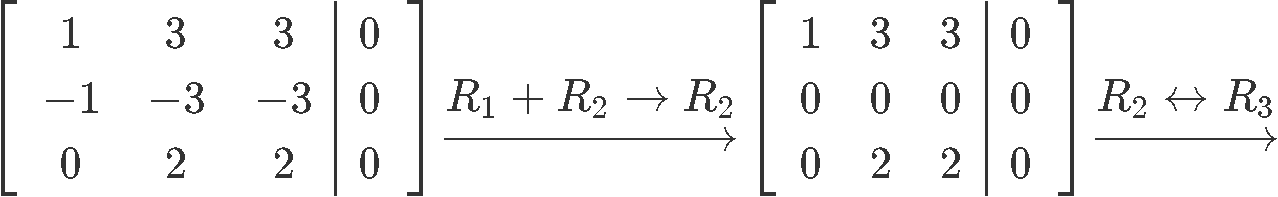
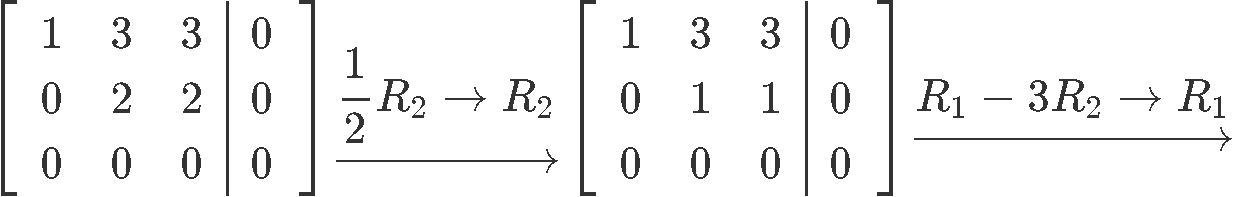
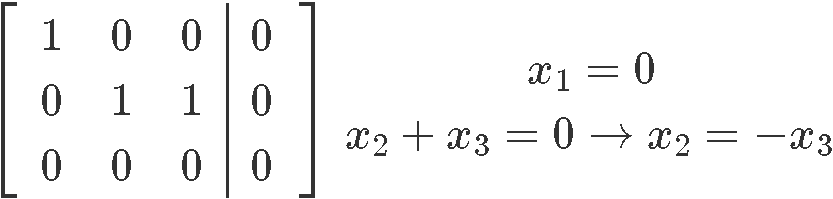
As you lot tin can see from the results above, $x_{3}$ happens to be a gratis variable since there is no pin corresponding to its column in the augmented matrix. And then, the concluding solution set for system of equations shown in equation x is:

Equation 4: Final solution set in parametric form

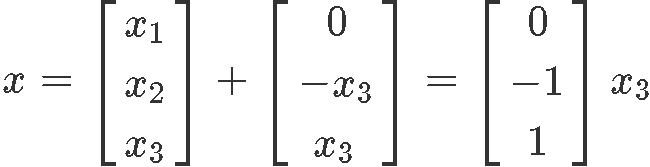
Example 2

Given matrix $A$ , find the solution gear up $Ax=0$ in parametric vector form:

Equation v: Matrix A

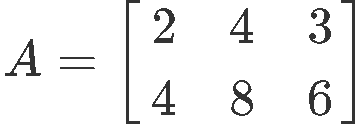
We write downward the matrix equation $Ax=0$ following the rules of matrix multiplication:

Equation 6: Matrix equation Ax=0

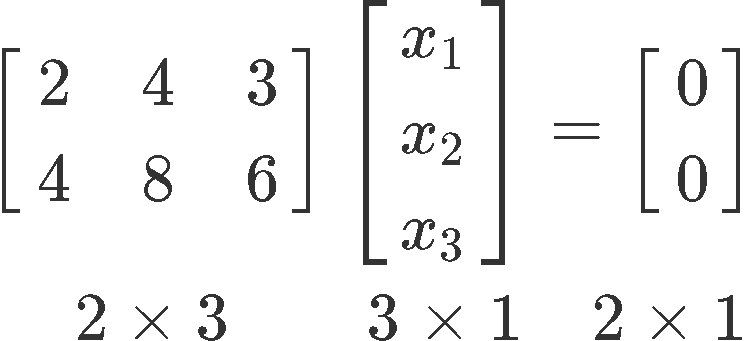
We employ this matrix equation to write an augmented matrix which we tin solve for the unknown variables every bit follows:

Equation 7: Reducing the augmented matrix

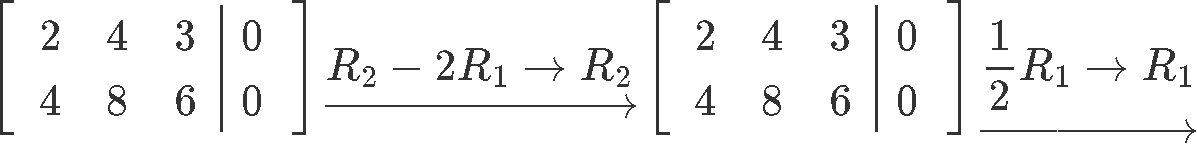
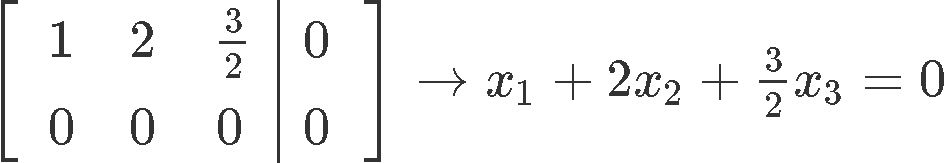
Past computing the reduced echelon course of the augmented matrix nosotros tin observe how we are left with no pivots for the 2d and third column, which means the variables $x_{two}$ and $x_{3}$ are complimentary variables. Then, we write the solution fix of linear equation 8 in parametric grade every bit shown below:

Equation eight: Final solution set in parametric form

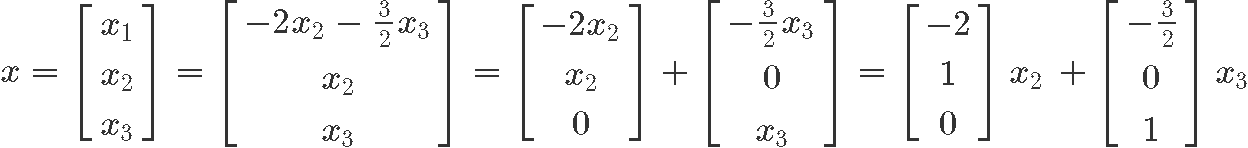
Example iii

Detect the solution set for the nonhomogeneous system in parametric vector grade:

Equation 9: Arrangement of linear equations

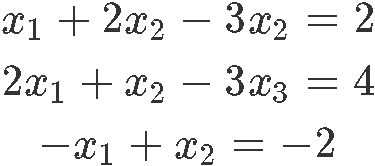
Writing down the corresponding matrix equation for the linear arrangement:

Equation 10: Matrix equation from the system of linear equations

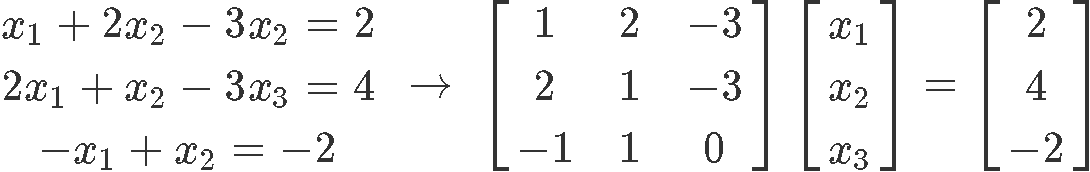
Nosotros convert this matrix equation into an augmented matrix and row reduce it into nosotros can obtain the unknown variables expressions:

Equation 11: Row reducing the augmented matrix

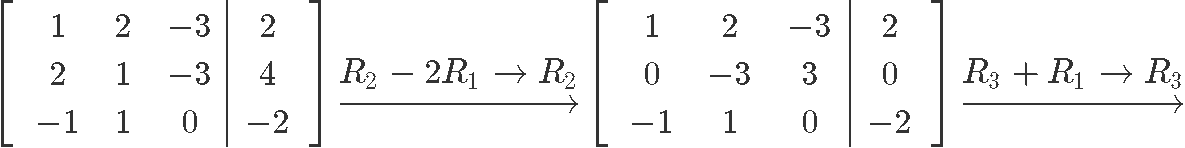
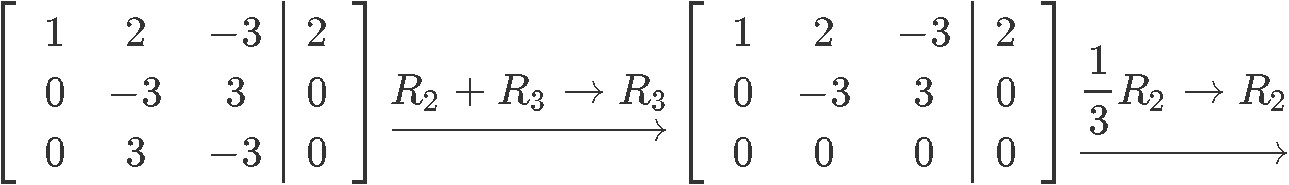
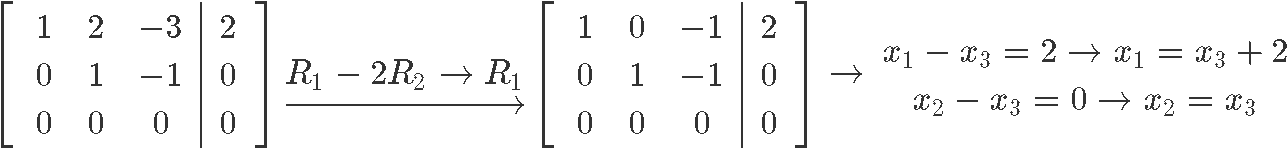
As you tin can see, the variable $x_{3}$ is a free variable and so the last solution prepare for this nonhomogeneous arrangement in parametric form is:

Equation 12: Last solution set up

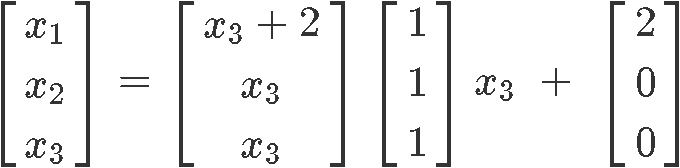
Notice how our final solution set contains an extra vector without a variable gene. This is usually the case for nonhomogeneous systems every bit you will run across in the next examples.

Case iv

Describe and compare the solution sets for each of the nest two linear equations:

$2x_{1} + 3x_{2} - 5x_{iii} = \,$ 0 $\;$ and $\; 2x_{ane} + 3x_{ii} - 5x_{iii} = \,$ 4

Equation 13: A homogeneous and a nonhomogeneous linear equation

For this instance, each equation happens to have its own solution prepare, and thus, we can obtain a matrix equation, then an augmented matrix to finally arrive to the parametric vector grade of the solution prepare with each equation.
Since we will be solving for the solution set of a linear equation at a time, let u.s. begin with the homogeneous equation (the one on the left in equation w). We get-go by writing downwards its corresponding matrix equation:

Equation 14: Matrix equation

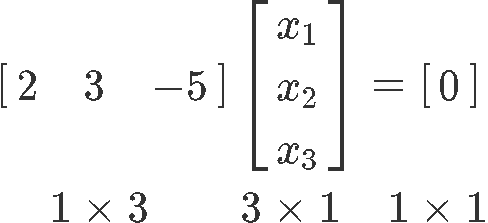
Although making a matrix equation out of a single algebraic equation may seem trouble some, nosotros merely have to follow the rules of matrix multiplication shown in equation ____ to construct the equation as has been shown above. The numbers in the bottom of the equation stand for the dimensions of each element in the multiplication: The first factor in the multiplication (the left-most matrix) has one row and three columns, followed past the adjacent factor with three rows and ane column. This makes sense since in order to multiply two matrices, the first one must contain the same number of columns as the second one has rows. And and so, the upshot of such multiplication must ever accept the dimensions coming from the number of rows from the offset matrix and the number of columns from the second matrix.

And so, the augmented matrix respective to the matrix equation above looks like:

Equation fifteen: Augmented matrix

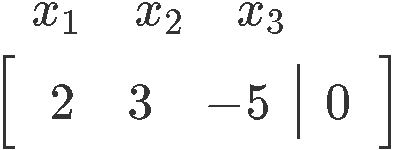
Observe we have written the names of the variables beingness represented in each column of the matrix, this, simply as the dimensions of the matrices in equation fourteen, is not needed. We have elected to write these specifications downward so the computations can exist shown clearly.
From the augmented matrix we can conclude that the variables $x_{2}$ and $x_{3}$ are complimentary variables. And and so, we write downwards the final solution set for this homogeneous equation:

Equation 16: Final solution set for homogeneous equation

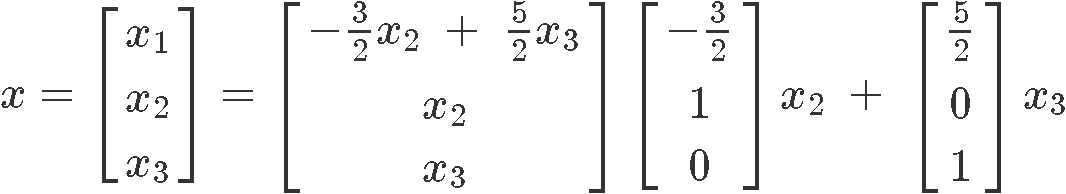
Now let us obtain the linear solution of the nonhomogeneous equation (the correct-most equation from the fix found in equation w) in parametric vector form. We start by writing downwards its respective matrix equation:

Equation 17: Matrix equation

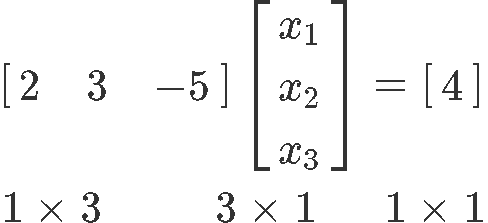
Which will produce the augmented matrix below:

Equation 18: Augmented matrix

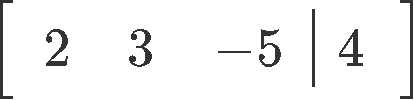
And the solution in parametric vector course is:

Equation 19: Last solution set up for the nonhomogeneous equation

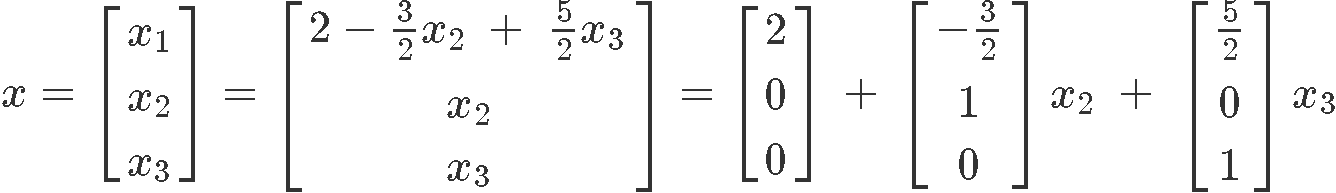
Notice that the deviation betwixt the two solutions (equations sixteen and 19) is only an extra vector resulting from the nonzero value of the nonhomogeneous equation.

Case 5

For this problem we are going to follow the exact same procedure equally we did in the past example to solve the set of linear equations provided. To facilitate the comparison between the two results, nosotros have designed a tabular array in which we have inputted the computation upshot of each step of the process:

$x_{1} - 4x_{two} + 2x_{3} = \,$ 0 $\;$ and $\; x_{i} - 4x_{2} + 2x_{three} = \,$ -three

Equation xx: Set of linear equations provided

Now let united states go through the entire process of the solution set in algebra within the next table:

Table i: Summary of description and comparison of the process to obtain a solution fix from linear equations

Notice that variables $x_{2}$ and $x_{3}$ are free variables. And the difference betwixt the solution of each equation is that the nonhomogeneous equation produces an extra column vector on its parametric solution.

***

To continue the practise on solving a set of linear equations we recommend you to take a wait at these algebra notes on solutions and solution sets of linear systems, both links contain some more examples similar to the ones we have studied today.

It is the end of this lesson, see y'all in the next one!

Source: https://www.studypug.com/linear-algebra-help/solution-sets-of-linear-systems

Share this post